Shooting a Cannon

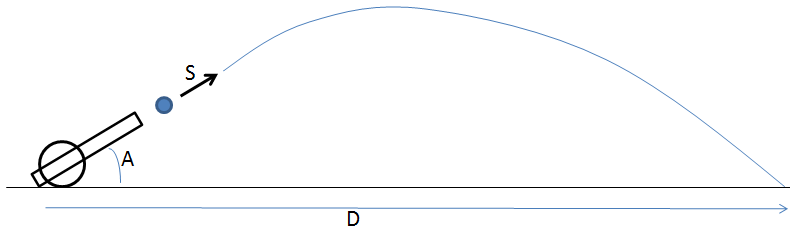
Let's use the laws of physics, to simulate the trajectory of a cannon ball. The cannon is tilted at angle A, and the ball comes out of the cannon with speed S. How far will it travel?

The ball's position is given by two coordinates, x and y. The ball's velocity has two parts, horizontal and vertical, Vx and Vy. After a short interval of time passes (Dt), the new position and velocity are given approximately, by:

x' = x + Dt×Vx
y' = y + Dt×Vy
Vx' = Vx (the horizontal velocity is unaffected by gravity)
Vy' = Vy - Dt×g

where g=9.8 is the force of gravity (m/s², in case you care about units).

Python program

We'll write a simple game where the user picks an angle, and shoots the cannon. Then we keep updating the ball's position, until it hits the ground. This occurs when y is exactly zero. In practice, this won't happen exactly, so we'll stop the trajectory when y gets negative.

The only remaining issue is, how do we get the initial Vx and Vy? It's just trigonometry:

Vx = Scos(A)
Vy = Ssin(A)

The sine and cosine functions aren't built into the language. We have to bring in the math library. Also, these functions expect the angle to be in radians, whereas the user probably entered the angle in degrees. So we'll have to multiply by π/180.

Here is the program:

import math

D = float(raw_input('Distance to target: '))
S = 50
Dt = 1
g = 9.8

while True:
    x = 0
    y = 0
    t = 0
    angle = float(raw_input('Cannon angle: '))
    angle *= math.pi / 180
    Vx = S * math.cos(angle)
    Vy = S * math.sin(angle)
    while y >= 0:
        x += Vx * Dt
        y += Vy * Dt
        Vy -= g * Dt
        print 'at t=',t, ': (x y)=(',x, y, ')'
        t += Dt

    if x > D:
        print 'you overshot'
    else:
        print 'you undershot'