Following is the story of my PhD work, back in France. This text is not to be taken too seriously. It was written long after my PhD was over and lack of seriousness is just there to mask the nostalgia for my student days. But this thesis was hard and laborious work, really…

Even if it involves nonfictional characters, like my advisor and other members of his group, they share absolutely no responsibility in what is said in these pages. This is my web page, and if it contains opinions, assertions and errors, they are mine, and mine alone.

Here is a quick overview of the saga:

In the beginning…

UNITY book My PhD advisor was Professor Gérard Padiou. I started to work with him in September 1992, in the school of engineering ENSEEIHT, part of the university INPT.

Gérard was at the time the head of a group working on distributed operating systems and distributed algorithms in general. At the time I joined, the group was beginning to look at distributed algorithms more formally. They had chosen the logical framework UNITY, proposed in 1988 by K. Mani Chandy and Jayadev Misra.

Basically, the UNITY framework is composed of four parts:

  • A (simple) programming notation, in which fair transition systems can be described in human readable form;
  • A (simple) logic, which can be seen as a fragment of linear-time temporal logic, but with only a limited number of operators, easy to understand and which cannot be nested;
  • A proof system, which can be used to prove that programs, described with the programming notation, satisfy properties, expressed in the logic;
  • An (infamous) substitution axiom, which introduces inconsistencies in the logic and allows one to prove properties much more easily (you start by proving that true=false, and the rest follows…).

To quote Jay Misra, who was paraphrasing Mark Twain, “The unsoundness of the the substitution axiom has been greatly exaggerated” (in his Note 14 on UNITY). However, and notwithstanding Jay’s protestations, the unsoundness was undeniable and resulted in really bad publicity for UNITY (especially among people who never read the book). One should keep in mind that:

  • Once the problem is solved, UNITY was clearly a novel and influential approach;
  • The statement and the study of the problem itself helped understand tons of things, especially with respect to composition.

In the end, the substitution axiom problem can be solved by adding 10 pages to a 516 page book. Once this is done, the book is definitely worth reading. As Beverly A. Sanders—who presented the first clean solution to the substitution axiom problem in her Formal Aspects of Computing article—once wrote: “As a practical matter, one can use UNITY for proving programs exactly as described in the book.” In this discussion, let’s forget about the substitution axiom and assume that UNITY is composed only of three parts: a programming notation, a logic and a proof system. The curious reader can read more on UNITY’s substitution axiom at the end of this page. Also, before I go further, note that everything I say here reflects my own ideas about UNITY, that none of it can be substituted (with or without the axiom) for Mani’s, Jay’s or Beverly’s thoughts, and that if you want to know what they think, you ask ‘em.

Back in Toulouse, Gérard and the other members of the group were ready to describe algorithms with the UNITY notation and to specify properties with the UNITY logic. But, being lazy people wanting to focus on distributed algorithms design and not on proofs details, they decided to hire a student to write a proof assistant for them. And that’s how I started my DEA work (a French DEA is a kind of MSc)…

“Click and prove!”

Dada On September 1st, 1992 (Ca ne nous rajeunit pas, tout ça…), I was given by Gérard a UNITY book, as well as an (outdated) manual of the Cornell Synthesizer Generator (later called Grammatech Synthesizer Generator). This tool can be used to generate a syntax directed editor for the language of your choice. What is needed is a description of the language through three grammars: input (the syntax), output (the display) and internal tree structure. At the internal level, using inherited and synthesized grammar attributes, you can do whatever computations you want, like type checking, code generation, or … correctness proofs!

The Cornell Synthesizer Generator (or, in short, the synthesizer) was shipped at that time with several examples, including code by Bill Pugh that showed how the tool could be used to prove properties on programs (pre/post-conditions on Dijkstra’s guarded commands language). My job, as given to me by my advisor, looked simple enough: modify and extend Pugh’s code to handle UNITY syntax and logic.

Indeed, it seemed so easy that I remember thinking at that time: “Let’s spend a month on the UNITY language and safety properties, and then we’ll have time to focus on liveness properties, which may be more difficult.” In other words, the whole thing would be ready for Christmas. Ah, the naiveté of my younger days…

I spent the first month going through Pugh’s code, which was not of the cleanest kind. Also, I had to learn UNITY and SSL (the synthesizer language) at the same time. What I got first were inconsistent results, including the ability to prove properties that were not valid (something that should definitely be avoided in program verification). After a month or so, I finally discovered that Pugh’s code was able to prove $A \lor B \Rightarrow A \land B$ as a valid formula!

I felt relieved that I was not crazy (Bill Pugh was, or at least a bit sloppy with his code), but not closer to finishing the whole thing done by Christmas. We quickly decided that to debug Pugh’s code would be too difficult a task and that we should instead find another existing procedure to check basic logical properties (again, the laziness pragmatism of the group: “Let’s find someone who has already done the job…”). This turned out to be a lot more difficult that we had anticipated.

At that time (Christmas came and went and we are now in early 1993), we could easily find two families of tools:

  • Firstly, theorem provers that could handle very complex logics, but wouldn’t prove anything unless you told them exactly how to do so (more aptly named proof assistants or, if you really want to be mean, proof editors). The first and best known of them was HOL. Others appeared later, like Coq or Isabelle (which were getting better at proving things on their own).

  • Secondly, theorem provers that could only handle more elementary logics, but were more automatized and could do (parts of) the job by themselves. A popular one, at that time, was Otter.

Because we were lazy, … Ok, you get the point.

So, I started to learn how to make Otter do proofs for me. Otter could work automatically, but only after its hundreds of parameters were carefully tuned, which required some expertise that none of us had. Nevertheless, mostly by trying random configurations (a time-honored strategy used by students all over the world), I managed to make Otter prove a few interesting things.

I had then to connect Otter to the editor generated by the synthesizer, which involved doing nasty things, like side-effects operations in grammar attribute evaluation to write and read in pipes and sockets. This made me write my first ever C program. That piece of code became (in)famous in the lab for a while, due to my peculiar C-programming style at the time: go to the next line only when you reach the end of the current line (80 characters or so), use plain numbers instead of fcntl.h macros, choose a, b, c, d, … as identifiers, don’t waste time writing comments, etc., kind of ioccc code without even looking for it. And, since it is clear that this kind of code will become unreadable after a week or two, I was in the habit of throwing away the source once the program seemed to work, only keeping the executable, which is why, unfortunately, I’m unable to show the source here. (Note that, a couple of years later, I was teaching C programming in operating systems labs in the same school, berating students for writing unreadable code.)

In the end, I was able to obtain a tool that could prove some elementary properties on a UNITY program, but only as long as very little arithmetic was involved. Otter, as a tool built by and for logicians, didn’t like numbers very much. For instance, the request to prove something like $(x < y) \land (x’ < y’) \Rightarrow (x+x’ < y+y’)$ on natural numbers would puzzle it for hours.

My tool was named DADA, for Distributed Algorithm Design Assistant. The name was proposed by a member of the group, whom I will not name, because this was pretty much his first, best and only contribution to the project. Note that, sadly, Google’s translation refers to the children toy and to the art movement, but not to my UNITY prover.

Experimenting with Dada made us realize that, when you describe distributed algorithms in UNITY, you deal with formulas that use at least as much arithmetic as they use logic. (Think of array indices, event counters, logical clocks, etc.) It took a while for researchers (not just us) to recognize the importance of arithmetic in program verification. This is why theorem provers like PVS had strong arithmetic modules and provers like Coq and HOL were later extended with arithmetic procedures.

Having become aware of the limitations of Otter for the type of formulas we had to prove, I started to look for a tool more inclined to work with numbers. (Trying to configure Otter to work with numbers was hopeless and all the help I could get from the logicians who knew the tool was: “You *do* know that integer arithmetic is undecidable, right?”.) The tool we soon found was called the Omega Calculator. Omega was not a theorem prover per se and was not intended to be used as such. Omega did one thing and one thing only: arithmetic. It was a decision procedure for Presburger arithmetic (linear integer arithmetic), written by a group led by… Bill Pugh! The return of the guy who was able to prove $A \lor B \Rightarrow A \land B$ scared us a little, but we decided to give him another chance. And we were right: Omega turned out to be very useful and helped improve Dada’s proving capabilities. (Note that a tool capable of proving $A \lor B \Rightarrow A \land B$ also improves proving capabilities, but that’s not the point.)

Helped by Abdellah El Hadri from the École Mohammadia d’ingénieurs, I managed to find a way to verify UNITY properties using Omega. What we did there was kind of a makeshift job, but it was later extended and properly formalized by Xavier Thirioux in his PhD work. Another (better) piece of C code, and Dada then presented the user with two ways to check properties. Depending on how much arithmetic was involved, a user could choose between Otter and Omega when checking a specific property. Omega was good with arithmetic (obviously), while Otter was good for large formulas (Omega, as a decision procedure, required a lot of memory). The choice was made by “clicking” on an Omega button, or on an Otter button, and then wait for the answer. The idea of being able to verify UNITY properties without further interaction—what we referred to as “click and prove!“™—was especially appealing to the lazy busy members of our group.

The use of Dada was most beneficial when looking for inductive invariants (more about those elsewhere). After a UNITY program and its desired properties are written in the tool, “finding the invariant” would be the name of the game. After each (informed) guess, Dada could tell you which transitions satisfied the invariant and which might not. The problematic transitions would then provide some insight as to why the predicate might not be an invariant. The whole process becomes iterative. Modify the invariant. Try again. Rinse. Repeat. Until the predicate is checked by Dada to actually be an inductive invariant. In practice, our dream of “click and prove!”, however, was more like “click and… wait and… try again!”.

The process can be short (when you are good at finding invariants, or lucky in general), or it can be long (when the invariant is especially tricky). For instance, the worst case in our experiments was the invariant in Friedemann Mattern’s termination detection algorithm: it took us almost two years to find that nasty half-a-page long predicate. Nevertheless, most of the time, using a tool like Dada to check the inductiveness of invariants saves time. Other forms of interaction with assistants are possible, but this basic principle of “guess and check” is still one of the most effective techniques (especially when using modern tools, much faster and more powerful than good old Dada).

The last thing for us to do was to publish a couple of papers. In order to help with this task, Dada was extended to be able to generate LaTeX from UNITY programs and specifications (in the end, generating LaTeX is what Dada was doing best).

This is what a Dada window looked like:

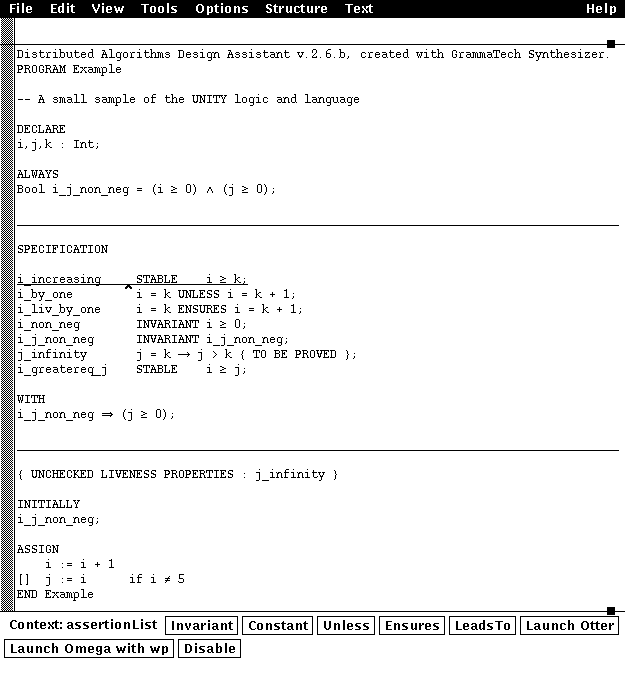
Besides this problem of proving formulas with arithmetic, our work on the Dada assistant made us understand (believe?) that we would need to improve some of the proof techniques used in UNITY before automatic tools like Otter or Omega could be used effectively. Our idea was that either you use a high-level tool, like HOL or Isabelle, capable of handling your whole verification problem, but then, you are really writing HOL or Isabelle proofs, not UNITY. Or you use more elementary and more automatic tools, but then you have to simplify the proof obligations at the level of your formalism, before attempting to use provers. Also, we knew that going more deeply into the design of a proof assistant would require an expertise in theorem proving that we did not have (don’t forget that we were interested in distributed algorithms to begin with).

Accordingly, and while I was still working on developing Dada during that time, the search for proof techniques specific to distributed algorithms started to become my real PhD work (as well as a topic of interest for most of the group). The idea was to find a number of abstractions, specific to distributed computing, that could be used to simplify proof obligations by reusing a generic form of reasoning related to these abstractions. The research project became Distributed Algorithm Design and Analysis (you don’t give up a name like that…)

Observer pour répartir

eye As a first specific aspect of distributed computing, we decided to focus on communication. In distributed algorithms, communication is generally described in terms of message passing, either point-to-point, or based on more elaborate schemes like broadcast and multicast. Processes “send” and “receive” messages which are transmitted reliably (or not), in order (or not) with bounded delay (or not). This model of communication in terms of messages is consistent with the reality of distributed computing: sending (or broadcasting) and receiving messages are the actual primitives used when distributed applications are implemented.

This model, however, corresponds to a very operational view of communication: what is described is what processes actually do to communicate. Operational descriptions are rarely good when it comes to reasoning and verification. We prefer to rely on more abstract and more logical descriptions. Ideally, we don’t want to describe what processes do to communicate, but rather the communication itself, i.e., what results from processes undertaking communication actions.

Furthermore, we would like an abstract description of communication to be easy to use in proofs and logical reasoning. This suggests that the abstraction be expressed logically and be well integrated with the other parts of the logic used in correctness proofs (in our case, the UNITY logic).

Finally, it should be noted than sending and receiving messages not only involves communication (transfer of data amongst processes) but also synchronization. For instance, processes can send and receive a non-valued token as a way to synchronize their actions. In this case, the point of the receive action (and, in the case of rendezvous, of the send action) is to block a process, not to transfer (explicit) data.

Our observation relation was based on these ideas. It is an abstraction of communication (only, not of synchronization), consistent with distributed architectures and reasonably well integrated with the UNITY language, logic and proof system.

Observations are integrated with UNITY in two different ways. Firstly, an observation can be a logical specification of communication. It can then be seen as a temporal operator that extends UNITY logic and can be mixed with other logical operators as part of proofs. Secondly, an observation can be a communication mechanism. It is then part of the operational description of an algorithm and can be considered as a new statement in the UNITY language. In the first case, we would speak of the observation relation; in the second case, of the observation mechanism.

Having observations both in the operational language and in the logic enabled us to derive observation relations (logical facts about the communication involved in an algorithm) from the operational description of an algorithm in which communication is described in terms of the observation mechanism. Then, the resulting observation relations could be mixed with other UNITY properties (other logical facts about the algorithm) to deduce the desired correctness properties. (This scheme may seem awkward and cumbersome, but it avoids compositional reasoning, for which there was (and still is) no good theory.)

The observation relation is defined as a reflexive, transitive and antisymmetric relation between state expressions. For expressions (of any type) $x$ and $y$, it is denoted by $x \prec\!\!\!\cdot\; y$. Intuitively, it means that values of $x$ are past values of $y$, those values being taken in the same order by both expressions. Also, some values of $y$ may never be taken by $x$, but $x$ eventually takes more and more recent values of $y$. Finally, the delay between a change in the value of $y$ and the corresponding (if any) change in the value of $x$ is unbounded. Expression $x$ is called the image of the relation and expression $y$ is called the source.

More formally…

Well, I won’t write the formal definition of observation, because:

  • it would require me to write quite a bit of other related stuff as well;
  • it’s already in the publications;
  • nobody cares anyway.

Let’s just say that, if $x$ is located on one process and $y$ is located on another, then the first process gets information from the second. This information may be outdated, but it doesn’t go back in time (w.r.t. information previously acquired) and it is guaranteed to eventually be updated to more recent information, even if there is no bound on how old the information may be. In other words, the two processes communicate, but the way this communication is actually achieved is not described explicitly.

This form of communication (unreliable, with unbounded delays) is easy to implement with message passing, which makes observations compatible with distributed architectures. Accordingly, one can always (well, almost always, there are some conditions) assume that a given observation relation is satisfied by a program. The relation then becomes part of the program description. This is what we called the observation mechanism. An observation, in this case, is considered a new statement in the UNITY language, which required us to modify UNITY’s operational semantics. Once this is done, processes can use the observation mechanism to communicate, instead of sending and receiving messages.

The nice thing about observation is that it is also a temporal operator, which can be mixed with other operators in specifications and proofs. For instance, as an example of a relationship between UNITY operators and observation, this can be proven as a theorem:

\[(p ~unless~ q) \land (q \prec\!\!\!\cdot\; p) \Rightarrow (p \mapsto q)\]

In that example, a liveness UNITY property ($\mapsto$, which is UNITY’s leads-to) is deduced from the conjunction of a safety UNITY property (unless) and an observation. This is made possible by the liveness component (“more and more recent values”) that is part of the observation definition.

Being able to use a single logical description for communication in algorithms, specifications and proofs actually helps in simplifying correctness proofs. Can we then conclude that our observation was a complete success?

Well, not exactly. Things work fine in proofs only if algorithms use the observation mechanism to communicate. Is it always possible to translate message passing communication into observation based communication? Technically, yes. However, the resulting description sometimes is not simpler than the original. In some cases, you cannot get rid of the FIFO sequences that are responsible for so much proof complexity when message based descriptions are used. When this is true, most of the benefits of using the observation mechanism is lost (but not all, see below).

From our experience, observation seemed to work well with monotonic variables. Actually, we have very few examples of observation based algorithms using non-monotonic variables. (One of these was a two-process handshake, based on mutual observations of two alternating single bits, somewhat similar to the Alternating Bit Protocol.)

If you are looking for a philosophical reason why observations work better with monotonic variables, I can suggest one (which the rest of the group did not really buy into): monotonic expressions implicitly contain their own causality (more below on observations and causality). Observation, like message passing, does no transfer causality (precedence relationships between events located on different processes). If needed, causality can be explicitly formulated (using, for instance, logical clocks). But these formulations are rather operational and tend to weaken the abstraction of observation. Unfortunately, we could not find a suitable abstraction for causal relationships. With monotonic variables, we don’t need one, and things work fine.

The good news is that distributed computing involves a lot of monotonic variables, such as clocks and event counters. Also, one can always replace a non-monotonic expression with a difference between two monotonic expressions. For instance, a channel between two processes (which is non-monotonic) can be replaced with the difference between the two histories (one on each process) of sent and received messages (which are both monotonic).

This idea was used by Paolo Sivilotti in his PhD. With his advisor Mani Chandy, they used a representation of communication based on a relationship between (monotonic) histories of message sent and received. The relationship they defined, which they called follows, looked very much like our observation, except that it was defined only for monotonic variables (which allowed them to get a simpler definition). In their case, communication is still described in terms of message passing, but in a more abstract and logical way. When I was at Caltech, working on compositional reasoning, I used (a modified version of) follows to describe communication between components.

For the record, I defended my PhD in November 1997, Paolo submitted his in December 1997, and we have never met. However, we both spent time at Caltech, working with Mani Chandy. We even used the same office (Jorg. 267), but at different times.

Product operator

product The second aspect of distributed programming we focused on during my PhD was the problem of so-called “true concurrency.” That there is a need for taking into account true concurrency is probably more debatable than the need to model communication. This is probably why only half the group showed interest in my work on a product operator. As a result, every time I talked about the product operator, half the folks in the group found the results interesting while the other half claimed that the problem I was solving did not exist in the first place (which makes it hard to convince them that the solution is interesting).

What is true concurrency, anyway? In many formalisms (including UNITY, TLA and most formalisms based on temporal logic), systems are described in terms of state transitions that represent atomic actions, and concurrency is expressed as interleavings of these atomic actions. To represent the fact that atomic actions A and B occur in parallel, we say that what actually occurs is equivalent to one of “A then B” OR “B then A”, without specifying which one. Another way to look at it is that nondeterminism is used to represent concurrency. True concurrency, on the other hand (also called non-interleaved concurrency), would be the case of A and B occurring simultaneously. This case is not taken into account in the standard interleaved formalisms.

Should one care about true concurrency? That’s where the debate begins. Some people say that overlapping of concurrent actions exists in the “real world”, and that true concurrency is a way to make a mathematical model closer to reality. Other people say that, if overlapping of actions becomes an issue, then the grain of atomicity used in the model must be changed to something finer.

Leslie Lamport once said (I think it was during a TLA$^+$ tutorial in Toulouse): If you want true concurrency in your model, you can just add it. In other words, even in a formalism based on interleaving (like Lamport’s own TLA$^+$), you can always add a specific action, say AB, to represent the simultaneous execution of A and B. Then, what can happen is “A then B”, “B then A” or “AB”, and true concurrency is taken into account.

What I did, through the definition of a product operation, was to ask (and partially answer) the following question: If additional statements are added to represent true concurrency, what happens? In other words, how different are the two models, with and without true concurrency. The answer I got (in the limited context of UNITY programs that use observations to communicate) is that both systems do not differ as much as one could expect.

The difference between a model with true concurrency, say TC, and a corresponding model without it, say IC, can be characterized by the properties that are true in IC but, because of true concurrency, false in TC. (Note that any property true in TC is also true in IC because IC uses a subsets of the possible transitions of TC.)

Consider the following simple example. A system consists of two processes A, with a state variable $a$, and B, with a state variable $b$. Both variables $a$ and $b$ are initially zero. Each process does a single thing before it stops: it assigns its variable with value 1. In the interleaving model, both actions cannot take place at the same time and one process must assign its variable before the other. In other words, a state where $a+b=1$ will occur. In UNITY, this is expressed by the property $a+b=0 \mapsto a+b=1$. This property is not satisfied by a model with true concurrency, in which it is possible that both processes assign their variables at the same time. This leads-to property is an example of a property true in IC but not in TC.

As a graduate student, I studied the case of distributed systems, described in UNITY, that used the observation mechanism to communicate. In this context, you can prove that safety properties like invariant (actually, always true, see the discussion of the substitution axiom below) are the same in both models, and that the leads-to properties that are true in IC and not in TC must have a global and transient right-hand side (like the $a+b=1$ in the example above). In other words, properties of the form $p \mapsto q$ will also be the same in both processes except, possibly, for properties where the predicate $q$ is global (it references several processes) and transient (it becomes false after it was true).

If you think about it, leads-to properties with a global transient right-hand side do not appear very often in distributed systems specifications, because in general, they cannot be observed. Therefore, for “useful” properties (invariants and observable leads-tos), systems IC and TC are equivalent and taking true concurrency into account or not is irrelevant (a result that does not help convince the people who thought that true concurrency need not be studied in the first place).

I first got the idea for the product operator while proctoring an exam. I then wrote a four-page paper for a French conference, RenPar’1996, which was rejected as a regular paper and accepted only as a poster. Annoyed by the fact that the reviewers didn’t understand what the paper was about, I decided that a longer paper would be better (four pages in the RenPar format was pretty short). Grumbling that I was going to write a real paper, with all the details, and publish it in a real conference, and that it would teach them, I embarked in the project of writing down a detailed proof. I soon realized that the “proof” I had in my notes was incorrect (it only worked if the processes never communicated!). This led to an interesting few weeks during which i) I could not think of a way to make the proof work in the presence of communication, and ii) I could not find any counterexample to the theorem “proved” in the RenPar paper. I kept going back and forth, looking for a proof on Monday, for a counterexample on Tuesday, back to a proof effort on Wednesday, and so on. This was one of the most exciting times of my PhD. I almost lost my mind. In the end, a long, ugly proof was published as a 20-page LNCS paper (probably my longest conference paper).

Observation, assignment and causality

corr Towards the end of my PhD work, I came up with a crazy idea. Crazy because:

  • It made a major component of my work, the observation relation, completely useless;
  • It confused the heck out of my advisor;
  • It turned out to be wrong.

The idea was that, because of the nondeterminism inherent to the UNITY model, observations were equivalent to plain, good old variable assignments. No need to bother defining a fancy $\prec\!\!\!\cdot$, just use $:=$ as is! The idea was not as absurd as it sounds, because assignments, within the UNITY model, involve delays, loss of values, and eventual refreshing of values, just like the observation. But the idea was also deeply disturbing, especially to my advisor, because assignments seemed too simple to make a good model of communication in distributed systems.

But I had a proof and managed to convince him that I was right. He went along, halfheartedly, and we decided to make this discovery the final chapter in my dissertation.

The French system of “doctorates” requires a candidate to have two external reviewers (called rapporteurs) approve his work as PhD work before he is allowed to defend. The reports that these reviewers write are quite important because they are a validation, besides publications and your advisor’s reputation, that the work has value. They are the first thing search committees members will look at (and often the last, unless they are brave enough to dig into the papers or, even braver, into the dissertation). I had two reviewers lined up (one with expertise in formal methods and another with expertise in distributed systems), but the formal methods guy insisted he needed my dissertation by the beginning of the summer (for a defense to take place in the fall). By the beginning of the summer, I was almost ready but not quite. Missing were the chapter on Dada and the proof of the equivalence between observations and assignments in the UNITY model. So, I gave this reviewer, alongside a draft of the dissertation, a paper that we had published on Dada and the proof sketch I had used to convince my advisor of the equivalence between $\prec\!\!\!\cdot$ and $:=$ .

In retrospect, it might have been safer to follow the example of an illustrious gentleman (also from Toulouse) and simply claim that I had a marvelous proof, too big to fit in the margin. Toward the end of the summer, as I was completing my writing, I realized that my proof was incorrect (a rather subtle mistake in an induction). As it had happened before with my product proof, I was left in limbo for a while, unable to find either a proof or a counterexample. This time, it was somewhat more stressful, with the defense approaching and the “theorem” already out to one of my reviewers.

In the end, I did find a counterexample, which was quite interesting. It turns out that if a process is only acquiring unrelated pieces of data from other processes, observations are indeed equivalent to simple assignments. However, this ceases to be the case if the various data observed are causally tied.

There are a few lessons here for graduate students:

  • One, writing your dissertation will take more time than you think.
  • Two, if your advisor cannot find the flaw in your work but insists that something is fishy, pay attention.
  • And three, write proofs, not “proof sketches”.

We decided that the whole thing was interesting enough to be included in the final dissertation. Instead of a ground-breaking theorem, the focus of the chapter became the relationship between observations, assignments and causality. Dealing with my reviewer was surprisingly easy: When I told him I had to make substantial changes to one chapter, he replied that he had not looked at it anyway. He added: “I don’t read proof sketches”. Interestingly, my formal methods reviewer thought this was the weakest chapter in the dissertation (nothing proved, really), while my distributed systems reviewer found it to be the most interesting (lost of insights). You simply cannot please everyone…

As an anecdote, I was back in Toulouse a few years later as a visiting professor, working with the same folks to model distributed systems (this time in TLA$^+$ instead of UNITY). As we were working on a model, someone in the group suddenly remarked: “But, aren’t we modeling communication with a simple form of assignment and don’t we already know from your work that it is incorrect to do so?” What happened then is:

  • Someone asked me why it was incorrect to do so.
  • I was unable to produce a counterexample right then and there.
  • Someone else grabbed a copy of my dissertation from the shelf and handed it to me.
  • I could not make heads of tails out of the chapter on observations, assignments and causality.

After retreating to a corner to read my own abstruse prose more carefully, I finally produced a counterexample, to the cries from the others of “that’s right, it’s all coming back to me now”. Either the difference between observations and assignments is subtle, or our dumb brains are wired to fall into the same trap over and over again.

A short note on the Substitution Axiom

As it is stated in the UNITY book (page 49):

If x = y is an invariant of program F, x can replace y in all properties of F. […] A particularly useful form of this axiom is to replace true by an invariant I, and vice versa.

The idea is that, if $I$ is an invariant of F, then it is always true in F, i.e., true in every state of every computation of F. Therefore, $I$ can be replaced by true anywhere it appears in properties without changing the truth of these properties.

In UNITY (as in other similar formalisms), a predicate $I$ is invariant in program F iff:

  • it is true initially in F, and
  • it is preserved by all transitions of F, i.e., the Hoare triple $\{I\}\,s\,\{I\}$ is true for all statements s of F.

Obviously, if a predicate is invariant, it is always true (by induction: it is true in the beginning and cannot be falsified). However, the converse is not true: A predicate can be always true in any state of any computation of a program and not be an invariant of that program.

The reason is that some states may not be reachable, i.e., they do not appear in any computation of the program, but still prevent a predicate from being invariant. A triple like $\{p\}\,s\,\{q\}$ does not take reachable states into account: If a state satisfies $p$ and statement $s$ is executed from that state, the resulting state must satisfy $q$, whether the state that satisfies $p$ is reachable or not. Now, if a predicate $I$ can be falsified by some statements only when they are executed from a non-reachable state, $I$ is not an invariant (from the definition of invariant). But it can still be always true in any reachable state of the program.

The following figure illustrates the situation when a predicate $p$ is always true but is not an invariant.

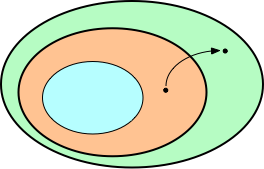
The green area is the set of all possible states; the blue area is the set of all reachable states; the orange area represents a predicate $p$.

The predicate $p$ is clearly always true (since all the reachable states are included in $p$). However, a transition like the one displayed, could start from a non-reachable state that satisfies $p$ and end in a state that does not satisfy $p$. If such a transition exists, then $p$ is always true, but is not an invariant.

Let $SI$ be the predicate that corresponds to the blue zone of reachable states ($SI$ is often called the strongest invariant because… well, it is!), then, because transitions cannot escape the blue zone, $SI$ is an invariant. So is $SI \land p$, because $SI \land p = SI$. Using the substitution axiom, we can replace $SI$ by true and deduce that $p$ is an invariant, which is not necessarily the case ($p$ is only always true). Hence the consistency problem in UNITY logic.

In other words, UNITY logic, without the substitution axiom, allows us to prove invariant properties. With the substitution axiom, it allows us to prove “always true” properties. But both are referred to as invariants. Since “always true” properties and invariant properties do not coincide, the logic becomes inconsistent.

In her paper, Beverly Sanders formally defines “always true” properties as well as the predicate $SI$. The resulting logic, which only deals with “always true” properties and does not care about invariants, is then consistent. Unfortunately, she keeps calling those properties invariant, which has led to a lot of confusion.

Furthermore, it turns out that both invariants and “always true” properties are important. It is rather obvious that always true properties are useful (we like to know what is true when a program is running) and that invariants can be used to prove them, but invariants are also of interest as properties because they can be used in compositional reasoning in a way that “always true” properties cannot.

Therefore, it seems that a logic should include both families of properties using, of course, a different name for each family. Personally, I like invariant and “always true”. The usage, in the world of temporal logic, is more to use invariants to refer to “always true” properties and inductive invariants to refer to what I call invariant properties. But not always. Lamport, in TLA$^+$, refers to invariants (my invariants) and invariance properties (my “always true” properties). Confusing, no? To avoid any ambiguity, one can always (invariantly?) talk of inductive invariants and non-inductive “always true” properties, but it can become rather tedious…